The center of intersection of the bisector of the triangle is also the center of the inscribed circle.
Bissectrix divide a triangle on three triangles is smaller, the total area of \u200b\u200bwhich, respectively, is equal to the area of \u200b\u200bthe original triangle.
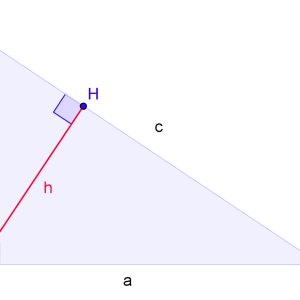
The heights of these triangles are the same and equal to the radius of the inscribed circle. Accordingly, in order to find out the radius of the inscribed circle, we need to learn the height of these triangles.
The height of these triangles can be obtained from the square formula, which looks like S \u003d 1/2 * A * H, where A is the base of the triangle, and H is the height, which in our case is R - the desired value.Remembering the formula for their tasks to obtain R \u003d H \u003d 2S / A, that is, the area of \u200b\u200bthe triangle is made half the base. The base of each of these triangles, respectively, is one of the sides of the main triangle.
- Get the perimeter by adding the parties.
- Divide the perimeter to 2 to get a half-meter.
- Split the triangle area on the resulting number.
In the simplest embodiment, the formula looks like R \u003d S / P.