The circumference is a geometric figure, acquaintance with which is still in preschool age. Later you will learn its properties and characteristic features. If the vertices of an arbitrary polygon lie on the circle, and the figure itself is located inside it, then you are geometric shape, inscribed in a circle.
The concept of radius characterizes the distance from any point of the circle to its center. The latter is located at the intersection of perpendiculars to each side of the polygon. Deciding with the terminology, consider expressions that will help to find a radius for any kind of polygon.
How to find a radius of the described circle - the right polygon
This figure can have any number of vertices, but all its parties are equal to each other. To find the radius of the circle, into which the correct polygon placed, it is enough to know the number of sides of the figure and their length.
R \u003d b / 2sin (180 ° / N),
b - the length of the parties,
N is the number of vertices (or sides) of the figure.
The reduced ratio for the case of a hexagon will have the following form:
R \u003d b / 2sin (180 ° / 6) \u003d b / 2sin30 °,
R \u003d b.
How to find a radius of the circle described - Rectangle
When a quadrangle is located in the circumference, having 2 pairs of parallel running parties and the internal angles of 90 °, the intersection point of the diagonals of the polygon and will be its center. Using the ratio of Pythagora, as well as the properties of the rectangle, we obtain the expression necessary for finding the radius:
R \u003d (√m 2 + L. 2)/2,
R \u003d D / 2,
M, L - Rectangle side,
D - his diagonal.
How to find a radius of the circle described - Square
We put in a circle square. The latter is the right polygon having 4 sides. Because The square is a special occasion of a rectangle, then it is diagonally also at the point of its intersection are divided by half.
R \u003d (√m 2 + L. 2) / 2 \u003d (√m 2 + M. 2) / 2 \u003d m√2 / 2 \u003d m / √2,
R \u003d D / 2,
m - sides of the square,
D - his diagonal.
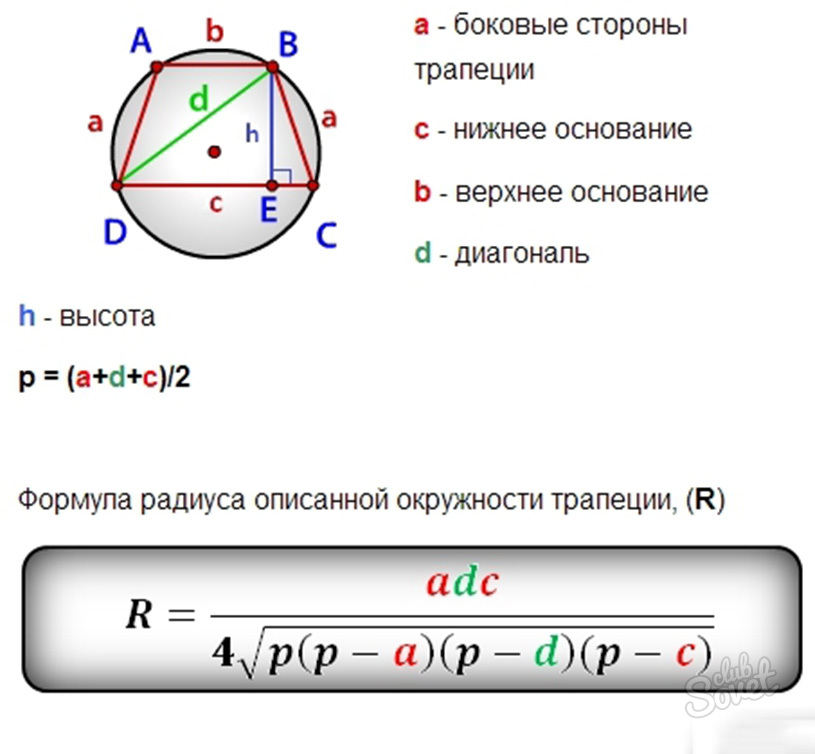
How to find the radius of the circumference described - an equilibrium trapezium
If the circle was placed in the circle, then to determine the radius, the knowledge of its sides lengths and diagonally will be required.
R \u003d M * L * D / 4√P (P - M) * (P - L) * (P - D),
P \u003d (M + L + D) / 2,
M, L - sides of the trapezium,
D - her diagonal.
How to find a radius of the circle described - Triangle
Arbitrary triangle
- To determine the radius of the circle describing the triangle, it is enough to know the magnitude of its parties.
R \u003d m * l * k / 4√p (p - m) * (p - l) * (p - k),
P \u003d (M + L + K) / 2,
M, L, K - triangle sides. - If the length of the side and the degree of the angle of the angle of the angles is known, then the radius is defined as follows:
For triangle MLK.
R \u003d m / 2sinm \u003d l / 2sinl \u003d k / 2sink,
M, L, K - triangle sides,
M, L, K - its corners (vertices). - In the presence of an area of \u200b\u200bthe figure, you can also calculate the radius of the circle in which it is placed:
R \u003d M * L * K / 4S,
M, L, K - triangle sides,
S is its area.
Isosceles triangle
If the triangle is a preceded, then 2 of it is equal to each other. When describing such a figure, the radius can be found in this ratio:
R \u003d m * l * k / 4√p (p - m) * (p - l) * (p - k), but m \u003d l
R \u003d M. 2/ √ (4m 2 - K. 2),
M, K - triangle sides.
Right triangle
If one of the corners of the triangle are direct, and near the figure is described a circle, then to determine the length of the radius, the latter will require the presence of known sides of the triangle.
R \u003d (√m 2 + L. 2) / 2 \u003d k / 2,
M, L - Kartets,
K - hypotenuse.