The circle is the visible set of multiple points that are at the same distance from the center. To find its area, you need to know what is a radius, diameter, number π and a circle.
The values \u200b\u200binvolved in the calculation of the area of \u200b\u200bthe circle
The distance bounded by the central point of the circle and any of the points of the circle is called the radius of this geometric shape. The lengths of all radius of one circle are the same. The segment between 2 by any circumference points, which passes through the central point is called a diameter. The length of the diameter is equal to the length of the radius multiplied by 2.
To count the area of \u200b\u200bthe circle, the value of the number π is applied. This value is equal to the ratio of the circumference length to the length of the diameter of the circle and has a constant value. Π \u003d 3,1415926. The length of the circle is calculated by the formula L \u003d 2πr.

Find the circle area through the radius
Consequently, the area of \u200b\u200bthe circle is equal to the product of the number π on the radius of the circle, erected into 2 degree. As an example, we will take the length of the circle radius equal to 5 cm. Then the area of \u200b\u200bthe circle S will be equal to 3.14 * 5 ^ 2 \u003d 78.5 kV. cm.

Circle area through diameter
Circle area can also be calculated, knowing the size of the diameter of the circle. In this case, S \u003d (π / 4) * d ^ 2, where D is the diameter of the circle. Take the same example, where the radius is 5 cm. Then its diameter will be equal to 5 * 2 \u003d 10 cm. Circle area S \u003d 3.14 / 4 * 10 ^ 2 \u003d 78.5 sq. Cm The result equal to the result of computations in the first example confirms the correctness of the calculations in both cases.

Circle area through the length of the circle
If the radius of the circle is viewed through the circumference length, then the formula will have the following form: R \u003d (L / 2) π. We substitute this expression in the formula of the circle area and as a result we obtain S \u003d (L ^ 2) / 4π. Consider the example in which the circumference length is 10 cm. Then the area of \u200b\u200bthe circle S \u003d (10 ^ 2) / 4 * 3,14 \u003d 7.96 square meters. cm.
Circle area through the side of the sides of the squeeze
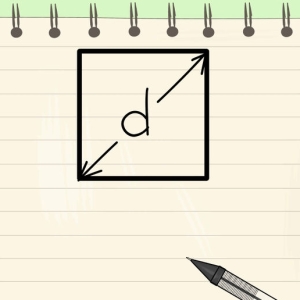
If the square is included in the circle, the length of the circle diameter is equal to the length of the square diagonal. Knowing the size of the sides of the square, you can easily find the diameter of the circle according to the formula: D ^ 2 \u003d 2a ^ 2. In other words, the diameter of 2 degrees is equal to the side of the square of 2 degrees multiplied by 2.
Calculate the value of the length of the diameter of the circle, it is possible to learn its radius, after which it takes one of their formulas for determining the area of \u200b\u200bthe circle.
Square of the Circle Sector
The sector is part of a circle bounded by 2 radii and arc between them. To find out its area, you need to measure the angle of the sector. After that, it is necessary to draw up a fraction, in the numerator of which will be the value of the sector angle, and in the denominator - 360. To calculate the sector area, the value obtained as a result of fractional fission must be multiplied by the area of \u200b\u200bthe circle calculated according to one of the above formulas.