How to find diagonal parallelogram

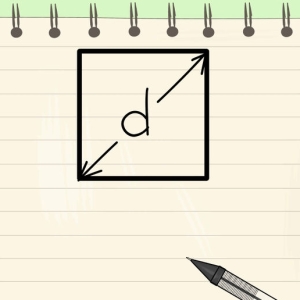
The quadrangle, opposite sides of which are parallel, is a parallelogram. Diagonal are direct connecting opposite vertices. The point of their intersection is the center of symmetry. In the general case, the parallelogram has two diagonals, D is long and d - short.

1

Find a diagonal parallelogram on the cosine theorem

To apply this method you need to know:

• The lengths of the sides of the parallelogram A and b.
• The cosine value of the angles of the parallelogram α and β.

D \u003d √a ^ 2 + b ^ 2 - 2ab · cosβ

d \u003d √a ^ 2 + b ^ 2 + 2ab · cosβ

D \u003d √a ^ 2 + b ^ 2 + 2ab · cosα

d \u003d √a ^ 2 + b ^ 2 - 2ab · cosα

2

Find diagonal parallelogram through one known diagonal and sides

To apply this method you need to know:

• The lengths of the sides of the parallelogram A and b.
• The length of one of the diagonals d or d.

D \u003d √2a ^ 2 + 2b ^ 2 - d ^ 2

d \u003d √2a ^ 2 + 2b ^ 2 - d ^ 2

d \u003d 2s / d · sinγ \u003d 2s / d · sinδ

4

Private case of determining the length diagonal parallelogram - Square

The square is a parallelogram in which all sides are equal and the angles are 90 °. Diagonal lengths in this case will be equal to D \u003d D and can be calculated by the Pythagoreo theorem.
D \u003d d \u003d a * √2

5

Private case of determining the length of the diagonal parallelogram - rectangle

The rectangle is a parallelogram in which the angles are equal and amount to 90 °. Diagonal lengths in this case will be equal to D \u003d D and can be calculated by the Pythagoreo theorem.
D \u003d d \u003d √ (a * 2 + b ^ 2)