In everyday life, we often have to compare fractional values. Most often it does not cause any difficulties. Indeed, everyone is clear that half of the apple is more than a quarter. But when it is necessary to write it in the form of a mathematical expression, it can cause difficulties. Apply the following mathematical rules, you can easily cope with this task.
How to compare fractions with the same denominators
Such fractions to compare most conveniently. In this case, use the rule:
Of the two fractions with the same denominators, but different numerics, the larger will be the numerator of which is greater, and the smaller is the numerator of which less.
For example, compare fractions 3/8 and 5/8. The denominators in this example are equal, therefore, apply this rule. 3 \u003c5 and 3/8 less than 5/8.
And indeed, if you cut two pizza by 8 stakes, then 3/8 shares are always less than 5/8.
Comparison of fractions with the same numerals and different denominators
In this case, the size of the number of denominators is compared. The rule should be applied:
If two fractions are equal to the numerals, then the more fraction, which is less denominator.
For example, compare fractions 3/4 and 3/8. In this example, the numerals are equal, it means that we use the second rule. The fraction 3/4 denominator is less than that of the fraction 3/8. Consequently 3/4\u003e 3/8
And indeed, if you eat 3 pieces of pizza, divided into 4 parts, you will be more wells than if you eaten 3 pieces of pizza, divided into 8 parts.
Comparison of fractions with different numerals and denominators
We use the third rule:
A comparison of fractions with different denominators should be made to comparing fractions with the same denominators. To do this, you must bring the fraction for a common denominator and use the first rule.
For example, you must compare the fractions 
and 
. To determine the larger fraction, we give these two fractions to the general denominator:
- we find the lowest total multiple (NOK) denominators of these fractions. Nok denominator fractions
and Number 6. - we find additional multipliers for both fractions. To do this, we divide our NOK to the denominators of both fractions. For the first fraction, an additional multiplier 6: 2 \u003d 3. Record it over the first fraction:
- Now find the second optional factor: 6: 3 \u003d 2. Record it over the second fraction:
- We multiply the fraction on your additional factors:
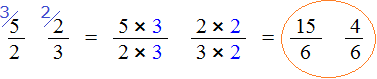
- So, we received two fractions with the same denominators. We apply the first rule and determine that:
- Consequently, 5/2 more fraction than the shot 2/3.
Check the video tutorial on the comparison of fractions:
0
732
