How to find a roll of a rectangular triangle

In life, we will often have to face mathematical tasks: at school, at the university, and then helping your child with homework. People of certain professions will face mathematics daily. Therefore, it is useful to memorize or remember mathematical rules. In this article, we will analyze one of them: finding the category of a rectangular triangle.

1
What is a rectangular triangle

To begin with, remember what a rectangular triangle is. The rectangular triangle is a geometric figure of three segments that connect points that are not lying on one straight line, and one of the corners of this figure is 90 degrees. The sides forming a direct angle are called categories, and the side that lies opposite the direct angle - hypotenuse.

2
Find a roll of a rectangular triangle

There are several ways to learn the length of the category. I would like to consider them more.

Pythagore's theorem to find a roll of a rectangular triangle

If we are known to the hypotenuse and catat, then we can find the length of the unknown category on the Pythagora theorem. It sounds like this: "The square of the hypotenuse is equal to the sum of the squares of the cathets." Formula: C² \u003d A² + B², where C is hypotenuse, a and b - catts. We transform the formula and get: a² \u003d C²-B².

Example. The hypotenuse is 5 cm, and roll - 3 cm. We transform the formula: C² \u003d A² + B² → A² \u003d C²-B². Next, we decide: a² \u003d 5²-3²; a² \u003d 25-9; a² \u003d 16; a \u003d √16; a \u003d 4 (cm).

Trigonometric ratios to find a roll of a rectangular triangle

You can also find unknown catt if any other side is known and any sharp corner of the rectangular triangle. There are four options for finding the catech with trigonometric functions: in sinus, cosine, tangent, Kotangent. To solve the tasks, we will help the table that is slightly lower. Consider these options.

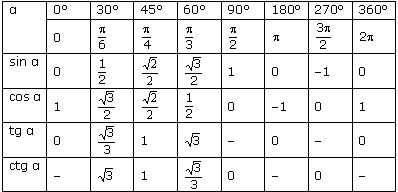
Find a roll of a rectangular triangle with sinus

Sinus angle (SIN) is the ratio of an opposite category for hypotenuse. Formula: Sin \u003d A / C, where a - catat, lying against this angle, and C is hypotenuse. Next, we transform the formula and obtain: a \u003d sin * c.

Example. Hypotenuse is 10 cm, angle A is 30 degrees. According to the table, calculate the sinus angle A, it is 1/2. Then, according to the transformed formula, we decide: a \u003d sin∠a * c; a \u003d 1/2 * 10; a \u003d 5 (cm).

Find a roll of a rectangular triangle with a cosine

Cosine angle (COS) is the ratio of the adjacent catech for hypotenuse. Formula: cos \u003d b / c, where b - catat, adjacent to this corner, and C is hypotenuse. We transform the formula and get: B \u003d cos * c.

Example. The angle A is 60 degrees, the hypotenuse is 10 cm. According to the table, calculate the cosine of the angle A, it is 1/2. Next, we decide: b \u003d cos∠a * c; B \u003d 1/2 * 10, b \u003d 5 (cm).

Find a roll of a rectangular triangle with tangent

Tangent angle (TG) is the ratio of the opposite catech to the adjacent one. Formula: TG \u003d A / B, where a is a cattet-taking to the corner, and B is the prigible one. We transform the formula and get: a \u003d tg * b.

Example. The angle is 45 degrees, the hypotenuse is 10 cm. According to the table, calculate the tangent angle A, it decreases: a \u003d tg∠a * b; a \u003d 1 * 10; a \u003d 10 (cm).

Find a roll of a rectangular triangle with the help of Cotangenes

Cotangenes Angle (CTG) is the ratio of the adjacent category to the opposing. Formula: CTG \u003d b / A, where B is a knitting knife, but the opposite. In other words, Cotangenes is "inverted tangent". We get: B \u003d CTG * a.

Example. The angle is 30 degrees, the opposite catat is 5 cm. According to the Tangent Table of the angle A is √3. Calculate: B \u003d CTG∠A * A; B \u003d √3 * 5; B \u003d 5√3 (cm).